|
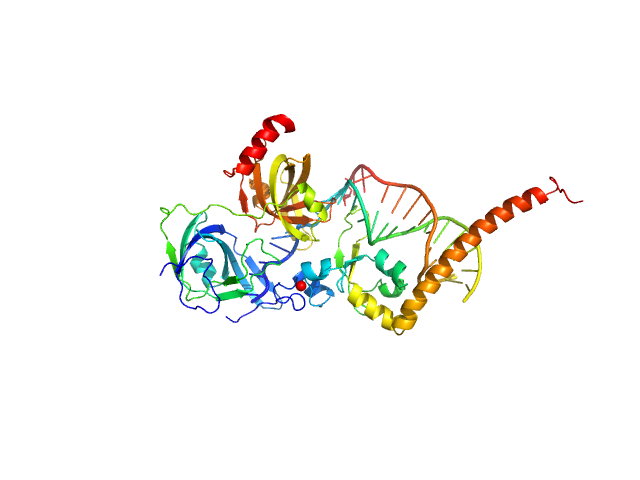
Synchrotron SAXS data from solutions of 5' Complex of XPA-DBD with RPA70AB in 20 mM Tris, 150 mM NaCl, 2% glycerol, 1 mM DTT, pH 7.5 were collected on the 12.3.1 (SIBYLS) beam line at the Advanced Light Source (ALS; Berkeley, CA, USA) using a Pilatus3 X 2M detector at a sample-detector distance of 1.5 m and at a wavelength of λ = 0.103 nm (I(s) vs s, where s = 4πsinθ/λ, and 2θ is the scattering angle). In-line size-exclusion chromatography (SEC) SAS was employed. The SEC parameters were as follows: A 50.00 μl sample was injected at a 0.50 ml/min flow rate onto a Shodex LW-803 column . Data measured from solute-free fractions and the sample-elution peak were normalized to the intensity of the transmitted beam and radially averaged. The scattering of the solvent-blank was subtracted from the sample peak data produce the data displayed in this entry.
Cell temperature = UNKNOWN. Storage temperature = UNKNOWN. Number of frames = UNKNOWN
|
|
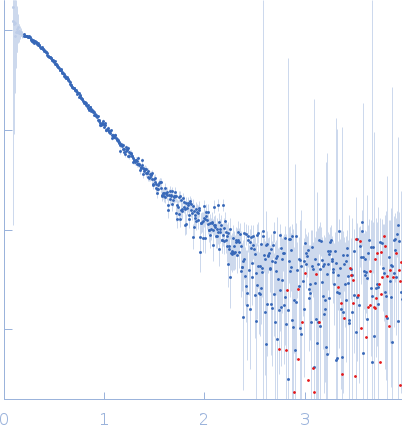 s, nm-1
s, nm-1